Евклидова геометрия

Eвкли́дова геоме́трия — геометрическая теория, основанная на системе аксиом, впервые изложенной в «Началах» Евклида (III век до н. э.).

Аксиоматика

Проблема полной аксиоматизации элементарной геометрии — одна из проблем геометрии, возникшая в Древней Греции в связи с критикой этой первой попытки построить полную систему аксиом так, чтобы все утверждения евклидовой геометрии следовали из этих аксиом чисто логическим выводом без наглядности чертежей.

 - В «Началах» Евклида, была дана следующая аксиоматика
 - От всякой точки до всякой точки можно провести прямую.
 - Ограниченную прямую можно непрерывно продолжать по прямой.
 - Из всякого центра всяким раствором может быть описан круг.
 - Все прямые углы равны между собой.
 - Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше - двух прямых.

Исследование системы аксиом Евклида во второй половине XIX века показало её неполноту.

В 1899 году Д. Гильберт предложил первую достаточно строгую аксиоматику евклидовой геометрии. Попытки улучшения евклидовой аксиоматики предпринимались до Гильберта Пашем, Шуром, Пеано, Веронезе, однако подход Гильберта, при всей его консервативности в выборе понятий, оказался более успешным.

Геометрия Лобачевского


Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.

Евклидова аксиома о параллельных гласит:

 - через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её.

В геометрии Лобачевского, вместо неё принимается следующая аксиома:

 -через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии и математики вообще.

История

Попытки доказательства пятого постулата

Поводом к изобретению геометрии Лобачевского явился V постулат Евклида - аксиома, эквивалентная аксиоме о параллельных. Он входил в список постулатов в «Началах» Евклида). Относительная сложность и неинтуитивность его формулировки вызывала ощущение его вторичности и порождала попытки вывести его из остальных постулатов Евклида.

Среди пытавшихся доказать были следующие учёные:
древнегреческие математики Птолемей (II в.), Прокл (V в.) (основывался на предположении о конечности расстояния между двумя параллельными),
Ибн аль-Хайсам из Ирака (конец X — начало XI вв.) (основывался на предположении, что конец движущегося перпендикуляра к прямой описывает прямую линию),
иранский математики Омар Хайям (2-я половина XI — начало XII вв.) и Насир ад-Дин ат-Туси (XIII в.) (основывались на предположении, что две сходящиеся прямые не могут при продолжении стать расходящимися без пересечения),
немецкий математик Х. Клавиус (1574),
итальянские математики 
П. Катальди (впервые в 1603 году напечатал работу, целиком посвященную вопросу о параллельных),
Дж. Борелли (1658), Дж. Витале (1680),
английский математик Дж. Валлис (1663, опубликовано в 1693) (основывался на предположении, что для всякой фигуры существует ей подобная, но не равная фигура),
французский математик А. Лежандр (1800) (основывался на допущении, что через каждую точку внутри острого угла можно провести прямую, пересекающую обе стороны угла; у него также были другие попытки доказательства).

При этих попытках доказательства пятого постулата математики вводили некоторое новое утверждение, казавшееся им более очевидным.

Были предприняты попытки использовать доказательство от противного:
итальянский математик Дж. Саккери (1733) (сформулировав противоречащее постулату утверждение, он вывел ряд следствий и, ошибочно признав часть из них противоречивыми, он счёл постулат доказанным),
немецкий математик И. Ламберт (около 1766, опубликовано в 1786) (проведя исследования, он признал, что не смог обнаружить в построенной им системе противоречия).

Наконец, стало возникать понимание о том, что возможно построение теории, основанной на противоположном постулате:
немецкие математики Ф. Швейкарт (1818) и Ф. Тауринус (1825) (однако они не осознали, что такая теория будет логически столь же стройной).


Создание неевклидовой геометрии

Лобачевский в работе «О началах геометрии» (1829), первой его печатной работе по неевклидовой геометрии, ясно заявил, что V постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий.

Утверждение геометрии Лобачевского

Лобачевский умер в 1856 году. Спустя несколько лет была опубликована переписка Гаусса, в том числе несколько восторженных отзывов о геометрии Лобачевского, и это привлекло внимание к трудам Лобачевского. Появляются переводы их на французский и итальянский языки, комментарии видных геометров. Публикуется и труд Бойяи.

В 1868 году выходит статья Э. Бельтрами об интерпретациях геометрии Лобачевского. Бельтрами определил метрику плоскости Лобачевского и доказал, что она имеет всюду постоянную отрицательную кривизну. Такая поверхность тогда уже была известна — это псевдосфера Миндинга. Бельтрами сделал вывод, что локально плоскость Лобачевского изометрична участку псевдосферы (см. ниже). Окончательно непротиворечивость геометрии Лобачевского была доказана в 1871 году, после появления модели Клейна.

Вейерштрасс посвящает геометрии Лобачевского специальный семинар в Берлинском университете (1870). Казанское физико-математическое общество организует издание полного собрания сочинений Лобачевского, а в 1893 году столетие русского математика отмечается в международном масштабе.

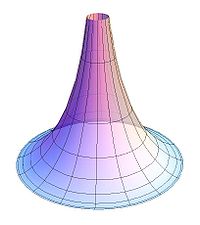
Псевдосфера
 
Итальянский математик Э. Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера. Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере.

Однако здесь даётся только локальная интерпретация геометрии, то есть на ограниченном участке, а не на всей плоскости Лобачевского.

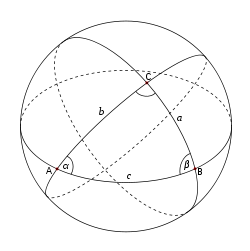
Сферическая геометрия Римана

Сферическая геометрия — раздел геометрии, изучающий геометрические фигуры на поверхности сферы. Сферическая геометрия возникла в древности в связи с потребностями географии и астрономии.

Основные понятия

Через любые две точки на поверхности сферы (кроме диаметрально противоположных) можно провести единственный большой круг — окружность, образованную пересечением сферы и плоскости, проходящей через её центр. Большие круги на поверхности сферы играют роль, аналогичную роли прямых в планиметрии. Любые два больших круга пересекаются в двух диаметрально противоположных точках.

При пересечении двух больших кругов образуются четыре сферических двуугольника. Площадь двуугольника определяется формулой S = 2R2α, где R — радиус сферы, а α — угол двуугольника.

Три больших круга, не пересекающихся в одной точке, образуют восемь сферических треугольников. Сферический треугольник, все стороны которого меньше половины большого круга, называется эйлеровым. Помимо трёх признаков равенства плоских треугольников, для сферических треугольников имеет место ещё один: два сферических треугольника равны, если их соответствующие углы равны.

Стороны сферического треугольника измеряют величиной угла, образованного радиусами сферы, проведёнными к концам данной стороны. Каждая сторона сферического треугольника меньше суммы и больше разности двух других. Сумма всех сторон сферического треугольника всегда меньше 2π. Сумма углов сферического треугольника s = α + β + γ всегда меньше 3π и больше π. Величина называется сферическим избытком. Площадь сферического треугольника определяется по формуле Жирара .

Соотношения между элементами сферического треугольника изучает сферическая тригонометрия

Вариации и обобщения

Двойной эллиптической геометрией Римана называют геометрию на сфере, в которой противоположные точки отождествлены; таким образом из сферы получается проективная плоскость.